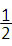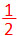|
หน้าแรก |
ป.1 - ป.6 |
ม.1 - ม.3 |
ม.4 - ม.6 |
O-NET |
สสวท. |
เพชรยอดมงกุฏ |
|
ห้องสอบ |
คลังข้อสอบ |
ป้ายโฆษณา |
ฝึกสมอง |
คิดเลขเร็ว |
E-BOOK |
|
Reading |
Listening |
สมุดจดศัพท์ |
เกมคำศัพท์ |
ผู้ทำเว็บ |
 |
กางเกงยีนส์ขายาวชาย กางเกงแฟชั่นผู้ชาย ใส่สบาย jeans 2 สี |
 |
แบบฝึกหัดข้อสอบ |
|
 | หน้าที่ผ่านมา | พื้นที่ หน้า 3 | หน้าถัดไป |  |
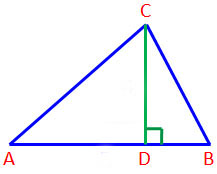
พื้นที่สามเหลี่ยม
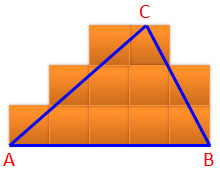 |
การปูกระเบื้องในรูปสามเหลี่ยมทำได้ยาก |
สามเหลี่ยมมีพื้นที่เป็นครึ่งหนึ่งของสี่เหลี่ยมมุมฉาก
ที่มีฐานและส่วนสูงเท่ากับสามเหลี่ยม
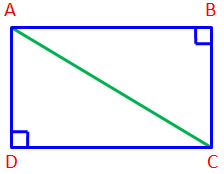 |
ABCD เป็นสี่เหลี่ยมมุมฉาก |
(ใช้ส่วนสูงร่วมกับสี่เหลี่ยม ABCD)
เนื่องจาก AC แบ่งครึ่งสี่เหลี่ยม ABCD
ดังนั้น สามเหลี่ยมมุมฉาก ADC
จึงมีพื้นที่เป็นครึ่งหนึ่งของสี่เหลี่ยม ABCD
 |
ABC เป็นสามเหลี่ยมมุมแหลม |
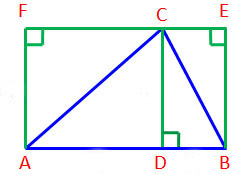 |
ลากเส้น AF ให้ตั้งฉากกับเส้น AB |
 |
ADCF เป็นสี่เหลี่ยมมุมฉาก |
 |
DBEC เป็นสี่เหลี่ยมมุมฉาก |
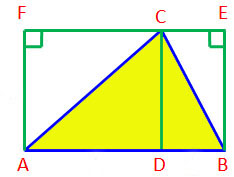 |
สี่เหลี่ยม ADCF + สี่เหลี่ยม DBEC = สี่เหลี่ยม ABEF |
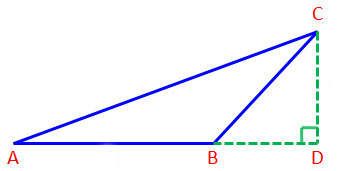
ABC เป็นสามเหลี่ยมมุมป้าน มี AB เป็นฐาน และ CD เป็นส่วนสูง
สามารถสร้างรูปสี่เหลี่ยมมุมฉากล้อมรูปสามเหลี่ยม ABC และ
พิสูจน์ว่าสามเหลี่ยมมีพื้นที่เป็นครึ่งหนึ่งของสี่เหลี่ยมที่ฐานและสูงเท่ากัน

ลากเส้น AF ให้ตั้งฉากกับเส้น AB
ลากเส้น BE ให้ตั้งฉากกับเส้น AB
ลากเส้น FC ผ่านจุด E และขนานกับเส้น AD
ได้รูป ADCF เป็นสี่เหลี่ยมมุมฉากล้อมรูปสามเหลี่ยม ABC
เส้น AB ยาว w หน่วย
เส้น BD ยาว m หน่วย
เส้น CD ยาว h หน่วย
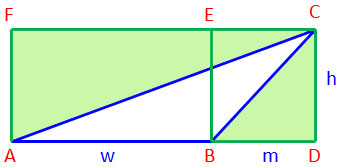
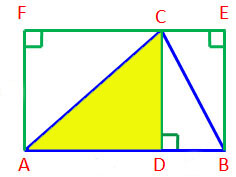
AC เป็นเส้นทแยงมุมของสี่เหลี่ยมมุมฉาก ADCF
เส้นทแยงมุมแบ่งครึ่งรูปสี่เหลี่ยมมุมฉาก
| ดังนั้น Δ ADC = | ครึ่งหนึ่งของสี่เหลี่ยม ADCF | ||||
| = |
| ||||
| = |
| ||||
| = |
|
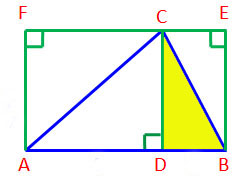
BC เป็นเส้นทแยงมุมของสี่เหลี่ยมมุมฉาก BDCE
เส้นทแยงมุมแบ่งครึ่งรูปสี่เหลี่ยมมุมฉาก
| ดังนั้น Δ BDC = | ครึ่งหนึ่งของสี่เหลี่ยม BDCE | ||
| = |
| ||
| = |
|
สามเหลี่ยม ABC = สามเหลี่ยม ADC - สามเหลี่ยม BDC ............ ( 5 )
แทน ( 3 ) และ ( 4 ) ลงใน ( 5 )
| สามเหลี่ยมมุมป้าน ABC = |
| ||||||
| = |
| ||||||
| = | ครึ่งหนึ่งของสี่เหลี่ยมมุมฉากที่มีฐานยาว w และสูง h |
สูตรคำนวณพื้นที่สามเหลี่ยม
จากตัวอย่างสามเหลี่ยมมุมฉาก สามเหลี่ยมมุมแหลม และสามเหลี่ยมมุมป้าน ที่ผ่านมาแสดงให้เห็นว่า| พื้นที่สามเหลี่ยม = | ครึ่งหนึ่งของพื้นที่สี่เหลี่ยมมุมฉากที่มีฐานและสูงเท่าสามเหลี่ยม | ||
| = |
|
 | หน้าที่ผ่านมา | พื้นที่ หน้า 3 | หน้าถัดไป |  |
 
|
คลังข้อสอบ
โจทย์แบบฝึกหัดและข้อสอบถูกรวบรวมไว้ในคลังข้อสอบ ครู/ผู้ปกครองสามารถเลือกโจทย์แต่ละข้อที่สอดคล้องกับเนื้อหาที่สอนในห้องเรียน
เพื่อนำมาร้อยเรียงกันเป็นชุดโจทย์ที่หลากหลายให้นักเรียนทำเป็นการบ้านหรือแบบฝึกหัด |
สงวนลิขสิทธิ์ตามกฏหมาย Copyright (C) 2011-2025 All rights reserved.