หน้าแรก |
ป.1 - ป.6 |
ม.1 - ม.3 |
ม.4 - ม.6 |
O-NET |
สสวท. |
เพชรยอดมงกุฏ |
ห้องสอบ |
คลังข้อสอบ |
ป้ายโฆษณา |
ฝึกสมอง |
คิดเลขเร็ว |
E-BOOK |
Reading |
Listening |
สมุดจดศัพท์ |
เกมคำศัพท์ |
ผู้ทำเว็บ |
 |
แบบฝึกหัดข้อสอบ |
|
 | หน้าที่ผ่านมา | สามเหลี่ยม หน้า 3 | หน้าถัดไป |  |
ผลบวกมุมภายใน 3 มุมเท่ากับ 180 องศา
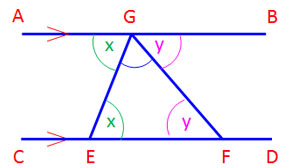
เส้นตรง AB ขนานกับเส้นตรง CD
ลากเส้น GE และ GF ได้ ΔEGF แนบในเส้นขนาน
มุม  AGE + มุมEGF
+ มุมFGB = 180° ..... | ( 1 ) | ผลบวกเป็นมุมตรง | |
| มุม AGE = มุมGEF ................................ | ( 2 ) | เป็นมุมแย้ง | |
| มุม FGB = มุมEFG ................................ | ( 3 ) | เป็นมุมแย้ง | |
| มุม GEF + มุมEGF
+ มุมEFG = 180° ..... | ( 4 ) | แทน ( 2 ) และ ( 3 ) ลงใน ( 1 ) |
ผลบวกมุมภายในของรูปหลายเหลี่ยม
ผลบวกมุมภายใน 4 มุมของรูปสี่เหลี่ยม = กี่องศา
ผลบวกมุมภายใน 5 มุมของรูปห้าเหลี่ยม = กี่องศา
ผลบวกมุมภายใน 6 มุมของรูปหกเหลี่ยม = กี่องศา
:
:
คำถามเหล่านี้ สามารถหาคำตอบได้โดยอาศัยคุณสมบัติของรูปสามเหลี่ยม
ตัวอย่างที่ 3
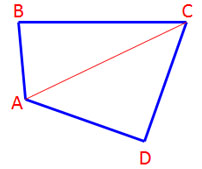
ABCD เป็นรูปสี่เหลี่ยมใดๆ มีมุมภายใน 4 มุม
ลากเส้นทแยงมุม AC เพื่อแบ่งรูปสี่เหลี่ยมออกเป็นรูปสามเหลี่ยม 2 รูป
สี่เหลี่ยม ABCD = ΔACB + ΔACD
ผลบวกมุมภายในของ ΔACB = 180°
ผลบวกมุมภายในของ ΔACD = 180°
ดังนั้น ผลบวกมุมภายในของสี่เหลี่ยม ABCD = 180° + 180° = 360°
ตัวอย่างที่ 4
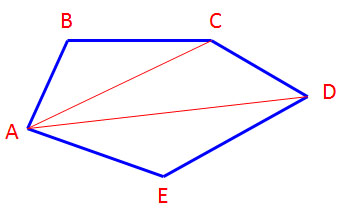
ABCDE เป็นรูปห้าเหลี่ยมใดๆ มีมุมภายใน 5 มุม
จากจุด A ลากเส้นทแยงมุม 2 เส้นไปยังจุด C และ D
รูปห้าเหลี่ยมถูกแบ่งเป็นรูปสามเหลี่ยม 3 รูป
ห้าเหลี่ยม ABCDE = ΔABC + ΔACD + ΔADE
ผลบวกมุมภายในของห้าเหลี่ยม = ผลบวกมุมภายในของสามเหลี่ยม 3 รูป
ผลบวกมุมภายในของ Δ แต่ละรูป = 180°
ดังนั้น ผลบวกมุมภายในของห้าเหลี่ยม ABCDE = 3 x 180° ° = 540°
จากตัวอย่างที่ 3 และ ตัวอย่างที่ 4 สรุปว่า
| 1) | จำนวนมุมภายใน = จำนวนด้าน เช่น |
| สี่เหลี่ยม มีด้าน 4 ด้าน มีมุมภายใน 4 มุม | |
| ห้าเหลี่ยม มีด้าน 5 ด้าน มีมุมภายใน 5 มุม | |
| 2) | สามารถแบ่งรูปหลายเหลี่ยมเป็นรูปสามเหลี่ยมหลายรูปโดยทำดังนี้ |
| 2.1) เลือกจุด 1 จุดเป็นจุดเริ่มต้น จากตัวอย่าง จุด A ถูกเลือกเป็นจุดเริ่มต้น | |
| 2.2) ลากเส้นทแยงมุมจากจุดเริ่มต้นไปยังจุดอื่น ๆ ให้ครบทุกจุด | |
| 2.3) จำนวนรูปสามเหลี่ยม = จำนวนเหลี่ยม - 2 เช่น | |
| ลากเส้นทแยงมุมแบ่งรูป 'สี่เหลี่ยม' เป็น Δ ได้จำนวน Δ = 4 - 2 = 2 รูป | |
| ลากเส้นทแยงมุมแบ่งรูป 'ห้าเหลี่ยม' เป็น Δ ได้จำนวน Δ = 5 - 2 = 3 รูป | |
| 3) | ผลบวกมุมภายในของรูป N เหลี่ยม = (N - 2) x 180° |
ตัวอย่างที่ 5
รูปหกเหลี่ยมด้านเท่า มุมภายในกางมุมละกี่องศา
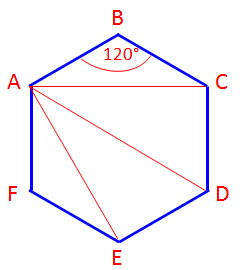
หกเหลี่ยมด้านเท่า มีด้านเท่ากัน 6 ด้าน
มีมุมภายในเท่ากัน 6 มุม
หาผลบวกของมุมภายในทั้งหกมุม
แล้วหารด้วย 6 เพื่อแบ่งเป็น 6 มุมเท่าๆกัน
เมื่อลากเส้นทแยงมุมแบ่งรูปหกเหลี่ยมเป็นรูปสามเหลี่ยม
ได้จำนวนสามเหลี่ยม = 6 - 2 = 4 รูป
ผลบวกมุมภายในของสามเหลี่ยมแต่ละรูป = 180°
ดังนั้น ผลบวกมุมภายในของหกเหลี่ยม = 4 x 180° = 720°
แบ่งผลบวกของมุมภายในออกเป็น 6 มุมเท่าๆกัน
แต่ละมุม = 720° ÷ 6 = 120°
| หน้าที่ผ่านมา | สามเหลี่ยม หน้า 3 | หน้าถัดไป | |
 |
ฝึกสมอง
ร่างกายของเด็กมีการเจริญเติบโตตามวัย เด็กที่ออกกำลังกายจะเติบโตเร็วและแข็งแรงกว่าเด็กที่ไม่ได้ออกกำลังกาย
กีฬาหรือการเล่นเป็นกิจกรรมที่ส่งเสริมการออกกำลังกาย สมอง ก็เช่นเดียวกับอวัยวะอื่นที่มีการเจริญเติบโตตามวัย
สามารถจัดกิจกรรมเพื่อส่งเสริมให้สมองเจริญเติบโตและทรงพลังมากกว่าปกติ
สมองทำหน้าที่หลายอย่าง เช่น การจำ, การคำนวณ, การคิดวิเคราะห์ ฯลฯ
การฝึกสมองทำให้สมองทรงพลังเหมือนการออกกำลังกายที่ทำให้ร่างการแข็งแรง
การฝึกสมองเพื่อเพิ่มความแข็งแกร่งให้สมองในแต่ละหน้าที่ต้องการกิจกรรมและเครื่องมือต่างกัน |
สงวนลิขสิทธิ์ตามกฏหมาย Copyright (C) 2011-2025 All rights reserved.